In the first two weeks of March 2016, three newspapers reported on 'the Curse of London': the strikingly high death rate among athletes who participated in the 2012 Olympic Summer Games in London. The newspapers reported that, of the 10,500 athletes who participated, 18 had died since the Summer Games, and that such a death rate was strikingly high. I thought it was striking, too. That is, the newspaper report, not the number, because the newspaper did not report what a non-striking, or 'normal' death rate among Olympians would be. Does 18 deaths out of 10,500 persons constitute an outrageous death rate, I wondered. I gathered some additional statistics and performed some calculations to test the hypothesis that 18 deaths is indeed a striking number.

The 2012 Olympic Summer Games took place from July 27 until August 12, so 3 years and 7 months have passed since. According to estimates from the US National Vital Statistics System, the average yearly death rates in the US per year, per age group, per 100,000 persons are as follows:

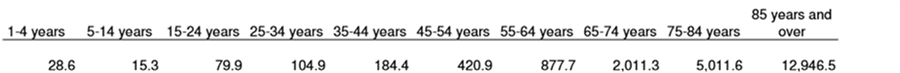
For the purpose of my calculations, I am going to make some assumptions. The numbers above are from 2007, and I am assuming that they are still representative. Also, Olympic athletes may not be the same as the average American, so I use the death rate among 15-24 year olds. The athletes of the Summer Games of 2012 were and are probably somewhat older than that, on average, but Olympian athletes may have a somewhat lower death rate than average US citizens of the same age.

Based on these statistics, we would expect that among 10,500 persons, in a period of 3 years and 7 months, the number of deaths, on average, would be (79.9/100.000) x 10,500 x (3+7/12) = 30.06 deaths.
Given what would be the ‘normal’ (average) rate, the hypothesis that the number of deaths among the Olympic athletes is a striking number can be statistically tested. To do that, we have to calculate the probability that this, or an even more extreme number of deaths occurs, over this period of time, given the average death rate. If the probability is below a preselected threshold (e.g., 0.05*), we reject the null hypothesis that the number of deaths is equal to the average, and we accept the alternative hypothesis: that the number of deaths is indeed striking.

Death rate distributions are modeled with the Poisson distribution (Zocchetti & Consonni, 1993). Using the Poisson distribution, we can calculate the probability of an event happening a specific number of times within a specific time interval, given the population average. With a population average of 30.06, the probability of observing 18 or fewer deaths is equal to 0.01. The probability of observing 18 or more deaths is .99. The probability of observing 18 deaths or less is obviously very low, even below the threshold. So, I reject the null hypothesis, and accept the alternative hypothesis that 18 is a striking number: a strikingly low number! I hereby refute the title of the newspaper report. I suggest that from now on we refer to 'The Blessing of London' instead.

* I am going to perform a two-sided test, because I am not sure if the observed number of deaths among the Olympic athletes is greater, or smaller than the average. Therefore, I have to divide the threshold for the probability by 2, and use .025 as the new threshold.